Lógó János

Azt szoktuk mondani, hogy a topológiaoptimálás a statika szobrászata: hogyan kell kialakítani egy nagy kődarabból egy formát úgy, hogy adott erők és megtámasztási feltételek esetén a legkisebb súlyú legyen, miközben megfelel mindenfajta szilárdsági, alakváltozási korlátnak, és ha lehet, még szép is. Mit csinál a szobrász? Lefarag a kőből. Mi is ezt csináljuk. Kiindulunk egy alakzatból, amit gondolatban földarabolunk rengeteg kis egységre, és ezekből a kis egységekből kell jó sokat eltávolítanunk.

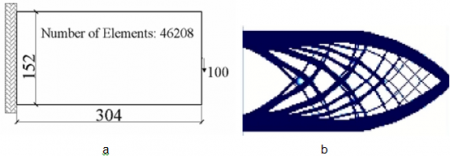
A számítógép a nagy alakzatból „kidobálja” a „kis” elemeket, azaz a szobrászhoz hasonlóan anyagot farag le, és a végtermék a „b” ábra. Be lehet bizonyítani, hogy az itt látható szerkezet (b ábra) az összes többi, azonos teherbírású szerkezetnél kisebb súlyú

A topológiaoptimálást sokan Anthony Michelltől eredeztetik, aki a huszadik század elején (1904) publikálta a legkisebb súlyú rácsos tartók tervezéséről szóló dolgozatát. De a történeti jelentőségű, „klasszikus” dolgozatok elolvasása után az a kép rajzolódott ki előttem, hogy az elsőség Clerk Maxwellé, aki mellett Michell Cambridge-ben dolgozhatott. Maxwelltől származik többek között a mechanika felcserélhetőségi tétele (az erőhatás és az alakváltozás helye felcserélhető egymással), de sokan inkább arról ismerik, hogy ő foglalta egységbe az elektrodinamika alapegyenleteit, és a Maxwell-eloszlás is az ő nevét viseli. Úgy látom, a világ az ő első topológiaoptimálási munkáit tulajdonítja Michellnek jelenleg, hiszen csak néhányan tudunk erről.

Engem Berke László, John Taylor – ők magyarok –, és Noboru Kikuchi kutatásai inspiráltak, de anspiráns vezetőmmel (Vásárhelyi Anna) és akkori tanszékvezetőmmel (Kaliszky Sándor) végzett kutatásaim is meghatározóak voltak pályafutásom során. Velük három évtizeden át publikáltam. Az optimálás, a szélsőérték-feladat megoldása a topológiában is alapvető, aminek szinten kiemelkedő matematikai alakja a lineáris programozás elméletének megalkotója, Farkas Gyula (J. Farkas), de a stochasztikus optimálásban nekem Prékopa András munkái lettek nagyon fontosak. Látható, hogy a magyarok nemzetközi szinten is az élvonalba tartoztak és tartoznak. Többen bekerültek például a NASA-hoz, ahol rendszerint titkosították a munkákat. Hosszú évtizedig alig jelentek meg dolgozatok publikusan, és sok összefüggést újra ki kell találni. Barta József, Kaliszky Sándor a mi tanszékünkön kutatott. Barta József fél évszázadnál régebbi munkáira még ma is hivatkoznak; tőle származik az alább látható topológiai példa a rudak elrendezésére. Itt kell megemlítenem Svéd Györgyöt, aki Ausztráliában publikálta híres topológiaoptimálási munkáját, ami szintén feledésbe merült.

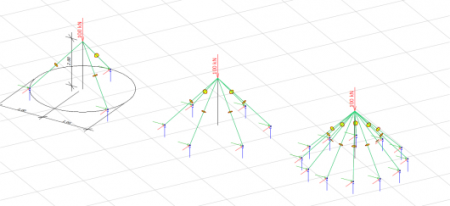Kevesebb rúddal is megtámaszthatjuk ugyanazt a szerkezetet, ugyanakkora erőhatás esetén

A topológiaoptimálás az 1980-as években gyorsult fel a számítástechnika fejlődése miatt. Ez utóbbi fél évszázadnak az egyik legismertebb magyar származású kutatója Rozványi György (G. I. N. Rozvany), akivel huszonöt évig dolgoztam együtt, többek között OTKA-kutatások kapcsán. Mostani kutatásaim során kiderült, hogy az alapvető elméletek már megvoltak az ötvenes években is, de korábban csak nagyon kis volumenű feladatokat tudtak megoldani. Néhány terület kutatása még ma is gyerekcipőben jár.

Hol használható a topológiaoptimálás?

Szinte mindenhol, mondjuk, a repülőgépgyártásban, az űrhajózásban, a biomechanikában. Egy beteg szétroncsolódott arccsontjait például egy optimálási feladat megoldása után pótolták. Tarnai Tibor kollégám a lótuszvirág szirmainak a topológiáját is vizsgálja. Vagy: hogyan tudjuk úgy felrakni a kis bőrdarabokat egy futball-labdára, hogy az alakja a lehető legjobban hasonlítson a gömbhöz? Egyrészt új formákat keresünk, másrészt meglévő formákhoz találunk elméletet, és megnézzük, hogy tényleg optimálisak-e ezek a formák. Ez utóbbi két kérdést témavezetésem alatt egy új NKFI-kutatásban is szeretnénk továbbvizsgálni Tarnai Tibor részvételével.

Az 1990-es években a Michigani Egyetemen dolgoztam. Az egyik ottani, japán származású tanszékvezető most a Toyota főkonstruktőre (director of Toyota Central R&D Laboratory). Vele azt vizsgáltuk például, hogyan kell kialakítani a Toyota csomagtartóját ahhoz, hogy kellő szilárdságú legyen, de minél több csomag elférjen benne.

Az is topológiai kérdés, hogy milyen legyen a bicikliváz, a repülőgép ajtaja, a repülőgép szárnya. Itt fontos tudni, hogy a sajátfrekvenciák elhangolásával elmozdulásokat akadályozhatunk meg. Közismert, hogy anyag vagy merevség (rugók) „hozzáadásával elvételével” – a sajátfrekvenciák megváltoztatásával – akár emberek súlyát is módosíthatjuk. Ugyanaz alatt az ember alatt nullát vagy akár kétszáz kilót is mutathat a mérleg, csak nagyon finoman kell rezgetni egy asztalt a mérleg lábai alatt. Dinamika-előadásokon ezt be szoktam mutatni a hallgatóknak.

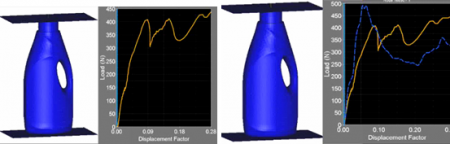Hogyan bírja a nagy terhelést az üveg úgy, hogy minél több folyadékot tölthessünk bele? Milyen formájú legyen a kupak, hogy könnyen le tudjuk tekerni?

A leendő NKFI-kutatásunkban egy fiatal kollégám azt vizsgálja majd, hogyan kell optimálisan csomagolni: hogyan kell kezelni a fonott szerkezeteket, hogy a csomag ne essen szét – a lehető legerősebb legyen a kötés, de minél kevesebb anyagból készüljön. Ez nagyon bonyolult topológiaoptimálási feladat.

Egy másik kutatásunk a stochasztikus alkalmazásokhoz vezet el. Ezekben a munkákban a tervezési bizonytalanságokat is figyelembe vesszük. Nem tudjuk például, hogy pontosan mekkora az erő, ezért eloszlással adjuk meg a nagyságát. Előfordul, hogy az erő támadáspontját sem tudjuk biztosan. Az eredmény mellé mindig megadjuk, hogy az adatok vagy a peremfeltételek alapján mekkora elvárt valószínűségi szinten érvényes az eredmény.

Mit jelent ez például az épületek esetében?

Bármennyire hihetetlen, egyetlen épületet sem terveznek száz százalékos biztonságra. Az épületeket – fontosságuk alapján – osztályokba sorolják, és mindegyik osztálynak megvan az összeomlási valószínűsége.

Az optimálás az építőiparban nagyon ritka, de például a kupolák lefedésekor optimálják a rudak számát – néhány forma el is terjedt. Sokszor felvetődik a kérdés, hogy hova kellene berakni rudakat, megtámasztást a kellő szilárdság eléréséhez, ezért a számítással nyert tapasztalatok a napi tervezési életben is hasznosulnak.

A topológiai feladat megoldása az esetek nagy részében azonban nem egyértelmű: ugyanarra a feladatra több megoldást is találhatunk (az előbb láttuk Barta József példáját). Ez jó, mert a tervezői szabadságot igazolja. A numerikusan kapott megoldások ellenőrzésében az analitikus megoldások segítenek, de az analitikus módszerek csak egyszerű feladatokban használhatók, mert rendkívül nehéz az eredmény kiszámítása. A gyakorlati szakemberek számára sokszor az is „optimum”, ha az új megoldás jobb az előzőnél: kevesebb anyag kell hozzá, és így olcsóbb. Ez, persze, matematikai értelemben nem feltétlenül optimum.

A badacsonyi Kisfaludy-kilátó

Néha én is átkerülök „a másik oldalra”. A badacsonyi Kisfaludy-kilátónak én voltam a felelős tervezője. A kilátó fönt van a hegytetőn, nem vezet hozzá közút. A természetvédők miatt helikopterrel sem vihettük oda az anyagot: mindent kézzel kellett fölvinni. A szerkezeten kívül el kellett készíteni az alaptestet is. Nemcsak a költségek, hanem a kivitelezhetőség miatt is minél kevesebb anyagot kellett beépítenünk, de a stabilitás az ellenkezőjét „igényelte”. Először 60 köbméterre jött ki az alapozás: ez 2,5 tonnával szorzandó, és az összes terhet kézzel kellett volna feljuttatnunk! Sikerült 23 köbméterre csökkentenünk az anyag mennyiségét. Ez is egyfajta optimum, de nem matematikai módszerrel jutottunk el hozzá, hanem mérnöki meggondolásokkal. A matematikai optimumkeresők általában úgy dolgoznak, hogy véletlenszerűen vesznek föl irányokat a paraméterek, összefüggések által meghatározott térben, és megnézik például, hogyan változik az építmény súlya, ha ezeknek a hatékony irányoknak a mentén haladnak. De nem elég, ha jó irányban indulnak el, mert a lépések hosszát is szabályozni kell: az sem jó, ha nagy a lépés, meg az sem, ha kicsi – különben elvétjük az optimumot. Tulajdonképpen ugyanúgy jártunk el, mint az algoritmusok – de a gyakorlatra támaszkodtunk.

Az új épületek alakja sokszor különleges formát követ.

Aki nem járatos a szakmában, azt hiszi, hogy a tartószerkezetük is különleges, holott a forma csak a homlokzaton jelenik meg, belül hagyományos mag van, ami a teljes terhet viszi. Azt mondtam korábban, hogy a topológiaoptimálás szobrászat – de ennek a fajta „épületszobrászat”-nak éppen az ellenkezője, ami most a gyakorlatban történik: mi erős szerkezetet szeretnénk csinálni, és ehhez keressük a formát.

Mikorra „válik felnőtté” az Önök tudománya?

Rettenetesen hamar: csak az a kérdés, milyen gyorsan megy át a gyakorlatba. Japánban, az Egyesült Államokban például gyorsan. Nagyon sok optimalizálási feladatot adnak a gyártók a biomechanika területén, többek között a protézisek kialakítására, de a kutatási eredményeket nem publikálják, hanem szabadalmaztatják. Ebből inkább a cégek – és szerencsére – a betegek profitálnak.

Silberer Vera